How to Find Percentile in Excel (PERCENTILE Function)

I am sure you have heard the word percentile when people talk about numbers and rankings.

I remember it being one of the ways we used to get our ranking in competitive exams. For example, if I get a 90% percentile score, it meant that I did better than 90% of the people who appeared for that exam.

While it could be hard to calculate percentile manually, with Excel, it’s super easy (and yes, Excel has an in-built function to calculate percentile).

Table of Contents

What is a Percentile?

A percentile is a value that tells you how many data points are below that specific percentile value. For example, in a dataset where the 50th percentile value is 10, it means that 50% of values in the dataset are below 10.

This is a useful statistical measure and I am sure you will hear and see it in action in multiple practical applications.

Let’s say that you have a group of people with ages 27, 32, 26, 38, 42, 31 and you want to know what’s the 50^th percentile of this group.

This means that you want to know what is a value below which 50% of values from a data set belong.

The answer, in this case, is 31.5. And if you look back on our data set, values 26, 27, and 31 are below 31.5, which is exactly 50% of the data set (3 values out of 6).

Now as I mentioned, you don’t need to do this manually as Excel has an in-built PERCENTILE function that would tell you instantly the percentile value.

Let’s see how to use this function in Excel.

Excel PERCENTILE Function

To find a percentile in Excel, you can use the PERCENTILE function. The parameters of the function are:

=PERCENTILE(array,k)

array – an array or range of cells with values for which we want to find the k-th percentile;
k – a percentile that we want to find (a percentage formatted as a decimal number between 0 and 1).

Apart from this function, which is available from Excel 2003 onwards, you can also use the following two, newer functions, available from Excel 2010:

PERCENTILE.INC – has the same parameters. All three functions use the calculated rank to sort values from a range. In case when there is non-integer rank for some value, this function will include this value. The calculated rank will be K*(N-1)+1;
PERCENTILE.EXC – In this case, the function won’t include the non-integer value, since the calculated rank will be K*(N+1).

In this article, you will see an example of the PERCENTILE function, as it is compatible with most versions of Excel.

Also read: How to Add a Percentage to a Number in Excel?

Calculating a Percentile in Excel

Suppose you have the below data set where there are scores in column A, and you want to find out the score that is the 90th percentile in this dataset.

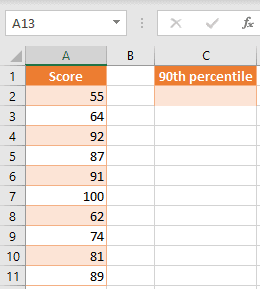
To get this, in cell C2, enter the formula:

=PERCENTILE(A2:A11,0.9)

In this example, the array consists of scores in range A2:A11, and k (percentile) is 0.9, as you want to find the 90^th percentile.

PERCENTILE formula to calculate 90th percentile

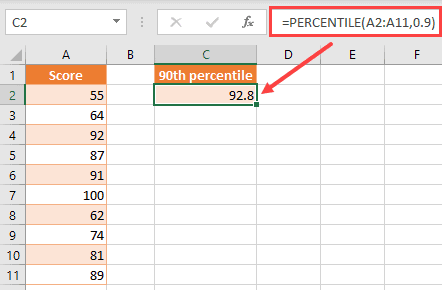
The result of the function is 92.8.

This means that 90% of the scores in a given data range (A2:A11) is below 92.8.

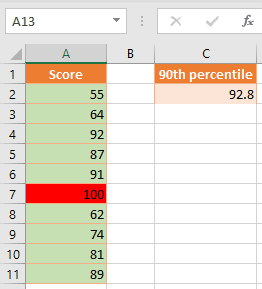
If you check in the data set, you will see that this is true, as only one score (in cell A7 – 100), is above 92.8, and all other scores (9/10 – 90% of them, are below).

highlighted Data that is above the specified percentile

This is often used to grade and rank students in a competitive exam. One benefit of using this method is that it takes the overall performance of the group.

For example, instead of telling me that I scored 90 out of 100, it tells me that I did better than 90% of the people.

The score in itself doesn’t tell me my position, as it could be an easy exam and many students might have scored more than 90. But the percentile instantly tells me my performance in comparison with the group.

Just like I used 0.9 as the argument to get the 90th percentile, you can use other values between 0 and 1 to get any percentile value.

For example, if you want the 50th percentile, then use 0.5 as the second argument in the formula.

Also read: Calculate MEDIAN IF in Excel

Things to Remember

The PERCENTILE function in Excel gives you a value below which is the certain percentage of values in a data set.

To calculate a percentile, you need to have a data set with at least one numeric value.

You also need to provide a percentile as a percentage of 0 to 100% or a decimal format (0 to 1).

If a percentile is between two values in a data set, the PERCENTILE function will interpolate values and return an intermediate value.

If any value in a data set is blank or non-numeric, the function will take it into the calculation as zero.

Also read: How to Calculate the Interquartile Range in Excel

Some Errors You May See when Working with Percentile Function

If the percentile parameter (k) of the function is not between 0 and 1, it will return the #NUM! error. If this parameter is non-numeric, you will get the #NAME? error.

In a case that the given data set (array parameter) doesn’t have any values and is empty, the function returns the #NUM! error.

I hope you found this tutorial about calculating percentile in Excel useful.

Other Excel tutorials you may also like:

2 thoughts on “How to Find Percentile in Excel (PERCENTILE Function)”

Eugene Kong

June 14, 2023 at 7:34 am

In the first example on age, 50% Percentile = 3/6 data = 31 yrs old. Next age is 32 yrs old. So the answer is 31.5 yrs old.
In the second exmaple, on score, 90% Percentile = 9/10 data = 92. Next score is 100. why is the answer, 92.8? why not 96?
- Steve Scott
  
  June 21, 2023 at 5:36 pm
  
  Hi Eugene… Percentile function doesn’t give you the mean between the Nth percentile value and the next value. So when we calculate 90 percentile, it gives a value below which 90% of the values would lie. It would not necessarily be a value from the dataset itself (such as 92.8). So if you change all the values in the dataset to 92 (except the 100 value), the 90% percentile value would still be 92.8